In my previous blog posting I have talked about how we count with decimal and binary numbers. As you have seen, we use the same concept here – a Reset-Carry operation. The only difference was the base – how many digits you have available for counting. In today’s blog posting I want to show you now how we can count with hexadecimal numbers. As you will see over the next months, hexadecimal numbers are very important for the implementation of our CPU.
The Hexadecimal Number System
The hexadecimal number system is in the first look quite different to the decimal or the binary system, because it contains digits AND letters for the representation of a number. The hexadecimal system provides you the following symbols that are used to represent hex values:
Digits 0 – 9
Letters A - F
Let’s count now with hex numbers up to 9:
00 Decimal 0000
01 Decimal 0001
02 Decimal 0002
03 Decimal 0003
04 Decimal 0004
05 Decimal 0005
06 Decimal 0006
07 Decimal 0007
08 Decimal 0008
09 Decimal 0009
What happens now when we want to count up to the hex number 10? Nothing! We don’t need to execute a Reset-Carry operation, because we have additional symbols available – the letters A to F:
09 Decimal 0009
0A Decimal 0010
0B Decimal 0011
0C Decimal 0012
0D Decimal 0013
0E Decimal 0014
0F Decimal 0015
We are now able to represent 16 different numbers within 1 position. That’s the power of the hexadecimal system. You would need 4 bits to accomplish the same in the binary system. When you now count up to the number 16, you also have to execute now a Reset-Carry operation:
0F Decimal 0015
00 Reset
10 Carry, decimal 0016
11 Decimal 0017
12 Decimal 0018
13 Decimal 0019
14 Decimal 0020
15 Decimal 0021
16 Decimal 0022
17 Decimal 0023
18 Decimal 0024
19 Decimal 0025
1A Decimal 0026
1B Decimal 0027
1C Decimal 0028
1D Decimal 0029
1E Decimal 0030
1F Decimal 0031
When you have now counted up to the hex value 1F, you have to execute again a Reset-Carry operation to count up to the next decimal value of 32:
1F Decimal 0031
10 Reset
20 Carry, decimal 0032
21 Decimal 0033
...
The reset-carry operation will happen over and over again until you run out of positions with your 2-hex value long number – then you have triggered a final overflow. In our case, the largest number that we can represent with 2 hex positions is the value of FF – decimal 255.
Base 16 System
Imagine now that we want to count the decimal sum of the hex number 1C3. In the first step we have to know the decimal value of each hex value:
0: Decimal 0
1: Decimal 1
2: Decimal 2
3: Decimal 3
4: Decimal 4
5: Decimal 5
6: Decimal 6
7: Decimal 7
8: Decimal 8
9: Decimal 9
A: Decimal 10
B: Decimal 11
C: Decimal 12
D: Decimal 13
E: Decimal 14
F: Decimal 15
Every decimal value is now multiplied with 16 and the power of its digit location. We apply here the same algorithm as we have applied with decimal numbers. The only difference is the weighting of each individual hex value. Therefore you can use the following formula to convert the hex value 1C3 to a decimal value:
(3 * 1) + (12 * 16) + (1 * 16^16) = 451
(3 * 16^0) + (12 * 16^1) + (1 * 16^2) = 451
3 + 192 + 256 = 451
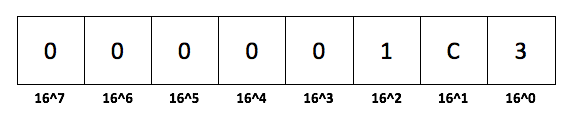
That’s the way how you perform a hex to decimal conversion.
Summary
In this blog posting you have seen how you count with the hexadecimal system. It’s not that hard, the only difference in the beginning is that you have digits and the letters A – F for counting available. But why do we need the hexadecimal system in computer technology? Because it’s powerful!
You can represent a 8-bit long value with just 2 hex position. For example, the binary value 11111111 would be the hex value FF. This is quite comfortable, because you just need 2 positions instead of 8 different ones. Easy, isn’t it?
Thanks for your time,
-Klaus
