In the next few blog posts I want to talk about some common stuff, which will be very important when we eventually design our CPU using transistors. In today’s blog post I want to cover counting with binary numbers. This might seems to be a very boring topic, but it is one of the most important things and you will need to know it without having to think about it. Before we get down to binary numbers, let’s review how we actually count with those well-known decimal numbers.
Counting with decimal numbers – Reset-Carry Operations
Every day – maybe even every hour – you are count with those decimal numbers: you count how many coffees you have had so far today, you count how many hours you have worked, you count how much money you have spent over the course of the day. But how do we do that counting at the technical level?
With decimal numbers we have 10 different digits: 0 to 9. Imagine you want to count up to number 9, using 4 possible digit positions:
0000
0001
0002
0003
0004
0005
0006
0007
0008
0009
After you have reached number 9, you have a big problem: you are out of numbers, because adding 1 to the number 9 would introduce an overflow. Therefore you reset the right-most number to 0 and send a carry (the number 1) to the next left-based number, which gives you the number 10. This task is called a Reset-Carry Operation (as described in the amazing book Digital Computer Electronics from Albert Paul Malvino).
0009
0000 Reset
0010 Carry
And then you can continue counting up to number 19:
0010
0011
0012
0013
0014
0015
0016
0017
0018
0019
When you have reached the number 19, you are faced with the same problem again: the next number can’t be represented just with the right-most digit. Therefore you perform the reset-carry operation again:
0019
0010 Reset
0020 Carry
And then the counting continues:
0020
0021
0022
0023
...
Imagine that you have finally counted up to 99. What you do when you want to add one to 99? In the first step you reset the right-most number to 0:
0099
0090 Reset
Then you send the carry to the next left-based number and add. But when you add 9 + 1 you have another overflow.
0090 Reset
0000 Reset
Therefore you send the carry again to the next left-based number. In our case there is no left-based number anymore, and we introduce again a 1:
0100 Carry
And finally you have the correct value of 100.
Base 10 System
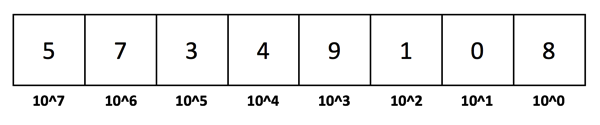
Because we deal with the numbers 0 to 9 in the decimal system, it has a base of 10. When you want to "calculate" the sum of a number, you just have to sum up the individual places according to their position. Imagine you want to calculate the decimal sum of the following number:
789
Of course we know that the sum is 789, because it is already described in the decimal system. But how do you calculate it? Let’s start again at the right-hand side of the number. The first digit has a weighting of 1, the next digit has a weighting of 10, and the third digit has a weighting of 100. So we can calculate the sum by calculating the individual weighting of every digit and finally sum up everything:
(9 * 1) + (8 * 10) + (7 * 100) = 789
(9 * 10^0) + (8 * 10^1) + (7 * 10^2) = 789
9 + 80 + 700 = 789
Easy, isn’t it?
Counting with binary numbers
Let’s discuss now how to count with binary numbers. With binary numbers we have only two possible digits: 0 and 1. In the context of electronics it could just indicate whether a current is flowing through an electrical circuit or not. Imagine now that we want to count with the digits 0 and 1 up to the decimal number 10. Counting up to 1 is very simple:
0000 Decimal 0000
0001 Decimal 0001
But when we want to continue to count up to decimal 2 we have a problem again, because we introduce an overflow within our Base 2 system. Therefore we perform another reset-carry operation here as well:
0001 Decimal 0001
0000 Reset
0010 Carry, Decimal 0002
And then we continue counting up to decimal 3.
0010 Decimal 0002
0011 Decimal 0003
Counting up to decimal 4 would again introduce an overflow, therefore we perform the reset-carry operation again:
0011 Decimal 0003
0010 Reset
0000 Reset
0100 Carry, Decimal 0004
When you count with binary numbers, you perform the reset-carry operation every 2 numbers, because you are dealing with a Base 2 system:
0100 Decimal 0004
0101 Decimal 0005
0100 Reset
0110 Carry, Decimal 0006
0111 Decimal 0007
0110 Reset
0100 Reset
0000 Reset
1000 Carry, Decimal 0008
1001 Decimal 0009
1000 Reset
1010 Carry, Decimal 0010
The reset-carry operation will happen over and over again until you run out of positions with your 4-bit long number – then you have triggered a final overflow.
Base 2 System
Imagine now that we want to count the decimal sum of the binary number 1010. We apply the same algorithm that we applied with decimal numbers. The only difference is in the weighting of each individual bit. The 1st bit has a weighting of 1 (if set), the 2nd bit has a weighting of 2 (if set), the 3rd bit has a weighting of 4 (if set), and the 4th bit has a weighting of 8 (if set).
(0 * 1) + (1 * 2) + (0 * 4) + (1 * 8) = 10
(0 * 2^0) + (1 * 2^1) + (0 * 2^2) + (1 * 2^3) = 10
0 + 2 + 0 + 8 = 10

You have just performed your first binary to decimal conversion! In another blog posting I will also show you the reverse conversion – decimal to binary.
Summary
In this blog post we reviewed how you can count with binary numbers. In the first step you saw how you perform the counting with decimal numbers, and finally we have transferred this process to binary numbers. The only thing that we have changed here was the base: instead of a Base 10 system we have just used a Base 2 system.
In my next blog posting we will have a more detailed look at the hexadecimal system - a Base 16 system. One of the nicest things of the hex system is that... – ooh no, let’s talk about that one the next time... 😉
Stay tuned,
-Klaus
